
本章教材始建於1998/9/17, revised: 2017/3/4
一、波浪性質
「波」是什麼東東﹕
- 波必須是週期性或近似週期性的運動﹔
-
波必然牽涉到某種性質在空間中傳播,波形傳播並不依賴介質之平移運動(如下圖 Mexican wave, 個別觀眾的動作只是依序站起、坐下而已,但是波形卻由左傳至右方)。
-
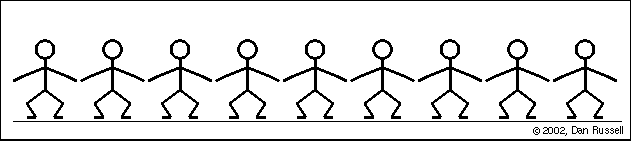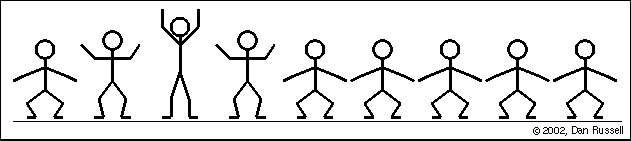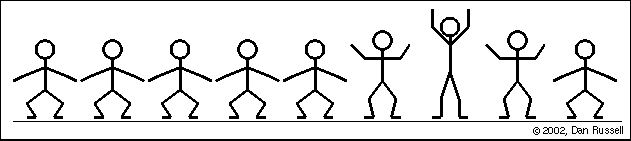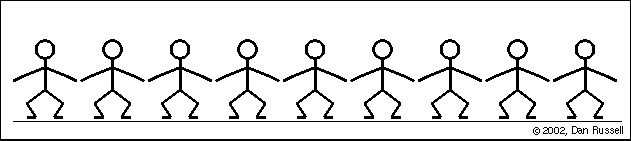
Mexican Wave (引自http://www.acs.psu.edu/drussell/Demos/waves-intro/waves-intro.html)
Mexican Wave (引自 Youtube https://www.youtube.com/watch?v=H0K2dvB-7WY ) (波形繞場一週,但各個介質--觀眾--仍在原位)
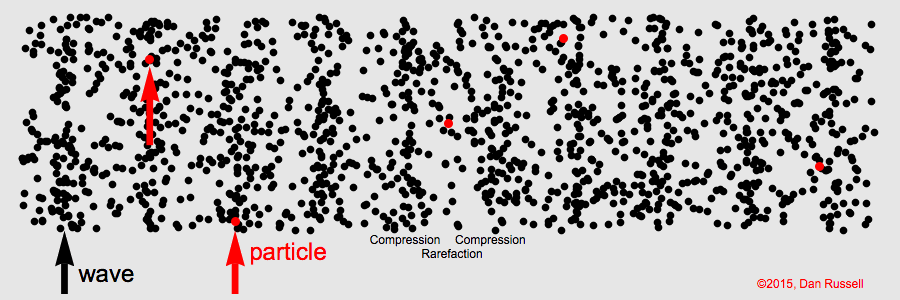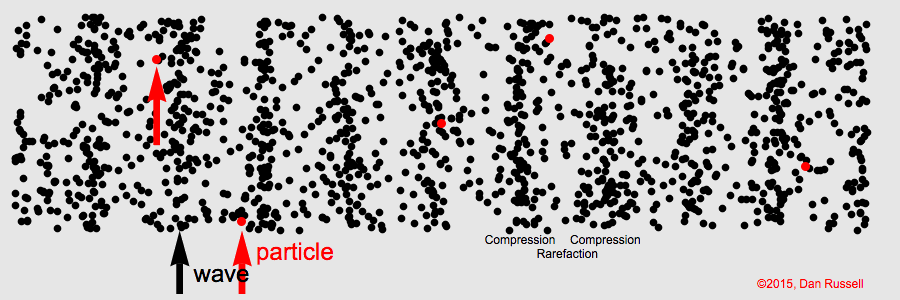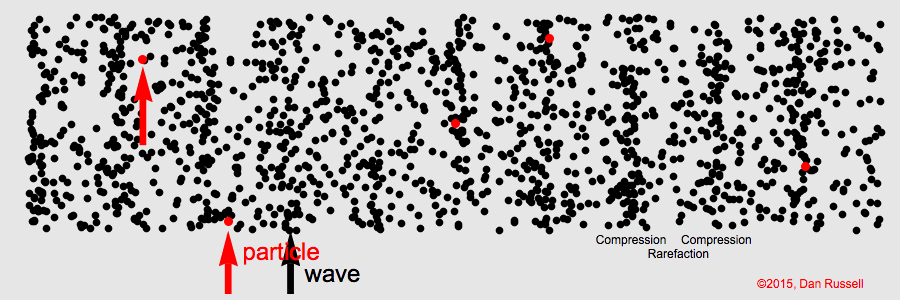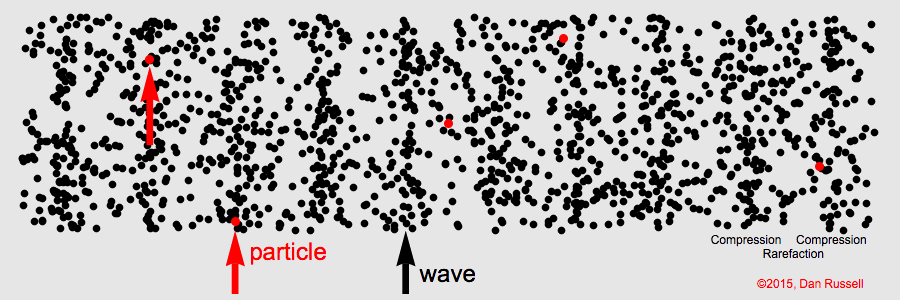
聲波藉空氣粒子疏密變化傳播之模擬動畫(引自http://www.acs.psu.edu/drussell/Demos/waves-intro/waves-intro.html)

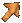 海洋中各種波浪之能量密度按照頻率大小依序排列之分佈情形(波浪能譜)。
波浪場大部份能量多集中分佈在十秒週期左右,長週期波浪在10-3秒處
之能量峰為海嘯與風暴潮所引起,最右側的兩個能量峰則分別為半日以及全日潮。
海洋中各種波浪之能量密度按照頻率大小依序排列之分佈情形(波浪能譜)。
波浪場大部份能量多集中分佈在十秒週期左右,長週期波浪在10-3秒處
之能量峰為海嘯與風暴潮所引起,最右側的兩個能量峰則分別為半日以及全日潮。
摘自Thurman, H. V. (1993) "Essentials of Oceanography", 4th ed.。
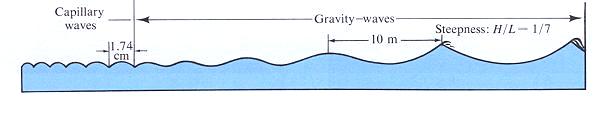
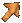 表面張力波(Capillary waves)以及重力波(Gravity
waves):當波長小於1.74cm時,表面張力效應較為重要,這種漣漪小波(表面張力波)具有圓形波峰以及V型波谷。當波長較長時,重力效應就變得比較重要,當波浪能量比較小時波形和正弦曲線非常相近,可是當波浪能量不斷增加,重力波的波形也會漸漸改變,會變為波峰變尖而波谷則變平坦的形狀,當尖銳度達到1/7或以上時波形就無法支撐而會發生碎波。摘自Thurman, H. V. (1993) "Essentials of Oceanography", 4th ed.。
表面張力波(Capillary waves)以及重力波(Gravity
waves):當波長小於1.74cm時,表面張力效應較為重要,這種漣漪小波(表面張力波)具有圓形波峰以及V型波谷。當波長較長時,重力效應就變得比較重要,當波浪能量比較小時波形和正弦曲線非常相近,可是當波浪能量不斷增加,重力波的波形也會漸漸改變,會變為波峰變尖而波谷則變平坦的形狀,當尖銳度達到1/7或以上時波形就無法支撐而會發生碎波。摘自Thurman, H. V. (1993) "Essentials of Oceanography", 4th ed.。
內波(Internal waves)﹕海水密度之垂直分佈具有分層構造(海水密度隨深度增加而遞增)時,則在水體內部也可產生重力波,這種波動便是內波,其週期與水體之密度分層狀況有關,週期之數量級為分鐘級。(本章第五節有更多關於內波的內容)
 |
|

由海底地震造成海嘯波之示意圖。摘自Thurman, H. V. (1993) "Essentials of Oceanography", 4th ed.。
海嘯數值模擬之動畫
|
|
Tsunami Propagation Animation - Andreanov |
|
|
|
|
|
Tsunami Inundation Animation - Aonae, Japan |
以上二動畫均摘自PMEL。 (和把石子投入池塘後產生的波況有何差別?)
慣性重力波(Inertial gravity waves)﹕當重力波的週期很長(~日,但小於當地地轉效應對應之週期)時、其所引起之水質點運動會受到地球自轉效應所影響,此種重力波稱為慣性重力波或是彭卡瑞波 (Poincare wave)。
行星波(Planetary waves)﹕週期很長(>日),波長也很長的波動,例如高空氣流線所顯示之波動以及造成黑潮或灣流呈蜿流時之波動均是。
 |
|
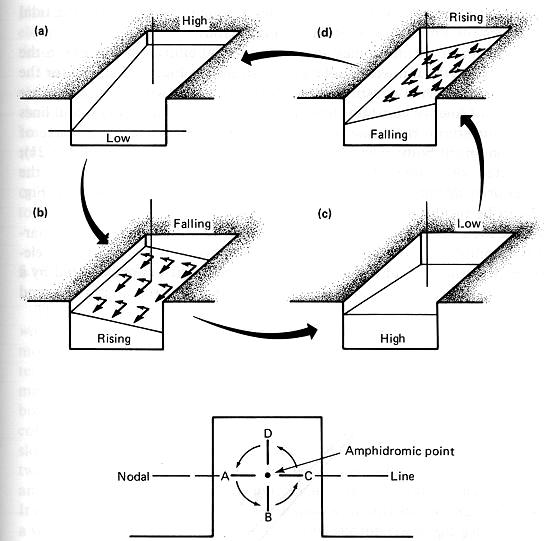
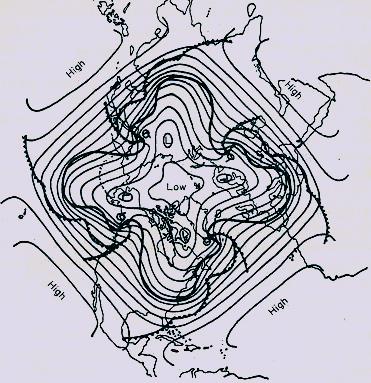
 在北半球的一個海盆中,由潮汐漲落所產生波動之示意圖。潮波會繞著無潮點
(Amphidromic Point)以反時鐘方向旋轉。摘自von Arx, W.S. (1962) "An Introduction
to Physical Oceanography"。
在北半球的一個海盆中,由潮汐漲落所產生波動之示意圖。潮波會繞著無潮點
(Amphidromic Point)以反時鐘方向旋轉。摘自von Arx, W.S. (1962) "An Introduction
to Physical Oceanography"。
-
波峰(Crest)﹕外觀波形之最高點。
-
波谷(Trough)﹕二波峰間最凹下部份稱之。
-
波高(Wave height):任一波峰與其相鄰波谷間之垂直距離,以H表示。
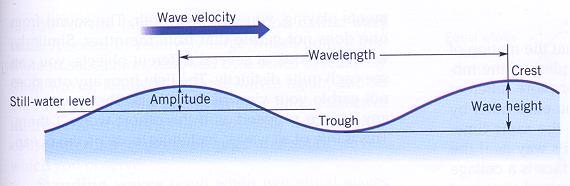
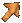 幾個與波形相關名詞之定義。
摘自Stowe, K. (1995) "Exploring Ocean Science", 2th ed.。
幾個與波形相關名詞之定義。
摘自Stowe, K. (1995) "Exploring Ocean Science", 2th ed.。
-
代表波高(Significant wave height)﹕又稱為示性波高,亦有人採用日譯稱為「有義波高」, 係海面上某瞬間,或是某點長時間連續觀測(如下圖),之所有波高中選取最大的 1/3 組平均後所得到的數值稱之,以H1/3 或Hs表示﹔據統計,Hs與海員目測之波高值甚為接近。
上圖中央紅線為所有波浪水位變化記錄之平均值,波浪曲線由下而上通過紅線之交點稱為「上跨零點」(up zero-crossing),每兩個跨零點之間為一個「波」(二點之時間差為此波之週期,而其間最高水位與最低水位之差值便是此波之波高),如此即可從波浪水位變化記錄求出一連串的波高與所對應週期之數據串,然後再將這二組數據串根據波高的大小按照由大而小的順序重新排列,這樣便可統計得出最大波高(及所對應之週期)、1/10代表波高(週期)、1/3代表波高(週期)、平均波高(週期)等用以描述波浪場狀況的統計數字。
-
波長(Wavelength): 波面上任意一點與其隨後波形上對應點之間的水平距離稱之,例如二相鄰波峰間之距離,以L代表。
-
波數(Wave number): 波長的倒數,常以k表示,k=2π/L,物理意義為波之密度,即沿波傳方向單位長度內波的數目(每2π相位是一個波)。
-
波尖銳度(Wave steepness): 波高與波長之比值H/L稱之,當此值過大時(> 1/7)波便會崩潰破碎。
-
靜水位(Still water level): 海面之平均水位,或是無波浪作用時之水位。
-
振幅(Amplitude): 波面最高點至靜水位之垂直距離,或是波高值的一半稱之。
-
週期(Period): 在一個固定點觀察一個完整的波形(一個波長)通過所需要的時間,以T表示。
-
頻率(Frequency): 週期之倒數稱之,通常以f表示,f = 1/T。頻率之物理意義為波之通量,即在單位時間內波形通過固定點的數目。
-
角頻率(Angular frequency): 週期之倒數乘以2π,常以ω表示,ω=2π/T。
-
波速(Wave speed): 又稱為相速度(Phase speed),係外觀波形移動的速度。如介質本身無平移運動 ,則波浪相速度 Cp = L/T = ω/k。
-
波群(Wave group)﹕海洋中外觀波形常呈現成群出現現象,即海面上有一長 列向同一方向傳播的波形。在某一固定點觀測時,例如首先出現一陣波高較小的時段,隨後波高漸漸增大,而在連續出現幾個大波後,波高又再減小﹔這種成群的波列即稱為波群。

 由船隻行進所產生的波浪 - 船波,便具有波群的特性。
由船隻行進所產生的波浪 - 船波,便具有波群的特性。
摘自Stowe, K. (1995) "Exploring Ocean Science", 2th ed.。
 鴨子游泳所產生的波形和船波呈現同樣的型態。
鴨子游泳所產生的波形和船波呈現同樣的型態。 -
群速度(Group velocity)﹕波群移動的速度稱之,係波能傳播的速度。 如介質本身無平移運動 ,則波浪群速度Cg=dω/dk。

 上圖為深水波相速度以及群速度隨頻率變化之關係圖。
圖中Cp最小值處所對應的頻率是一個重要的分界點,頻率低於此者屬重力波範圍(Cg < Cp),頻率高於此者則為表面張力波(Cg > Cp)。摘自Neumann, G. and Pierson, W.J., Jr. (1966) "Principles of Physical
Oceanography"。
上圖為深水波相速度以及群速度隨頻率變化之關係圖。
圖中Cp最小值處所對應的頻率是一個重要的分界點,頻率低於此者屬重力波範圍(Cg < Cp),頻率高於此者則為表面張力波(Cg > Cp)。摘自Neumann, G. and Pierson, W.J., Jr. (1966) "Principles of Physical
Oceanography"。-
深水波(Deep water wave): 水深比一半波長(L/2)深時稱之。
-
淺水波(Shallow water wave): 水深比廿分之一波長(L/20)淺時稱之。
-
自由波(Free Wave): 當波浪能夠不受外力影響而保持自由傳播狀態者稱之,例如 湧浪、海嘯均是。
-
強制波(Forced Wave): 波浪持續受到外力作用者稱之,例如風浪、潮汐等均是。
-
行進波(Progressive wave): 外觀波形以特定速度行進者稱之。
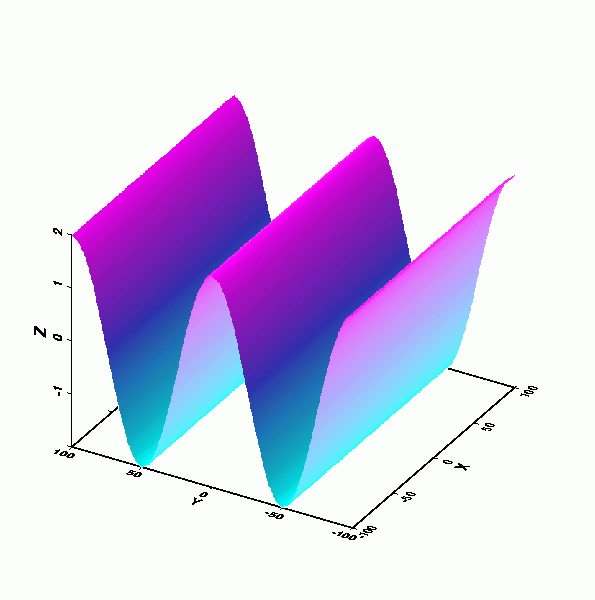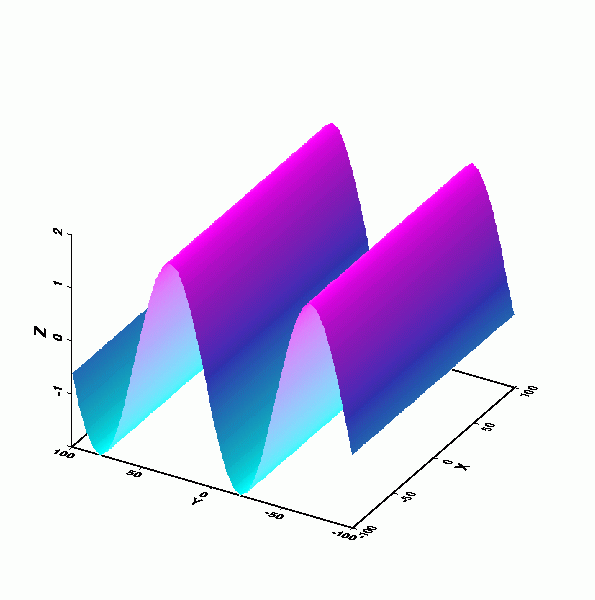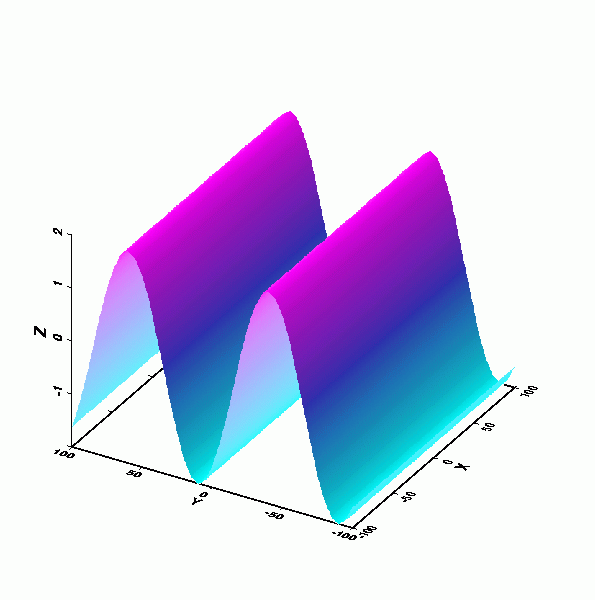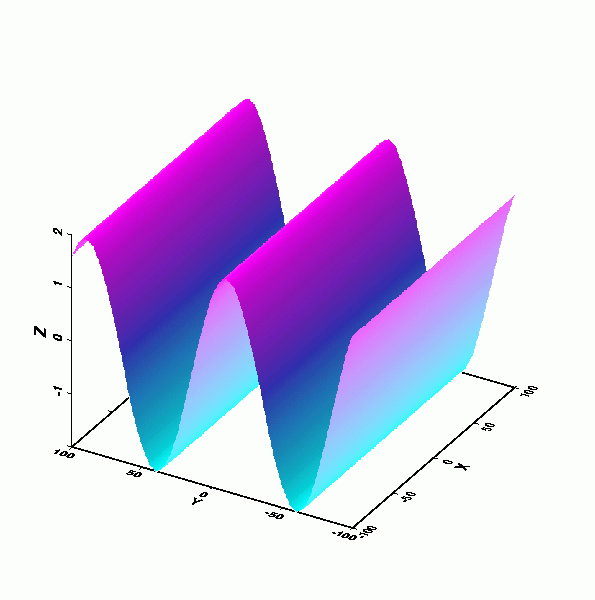
-
駐波(Standing wave)﹕外觀波形並無明顯之移動趨勢,各點僅有水面上下起伏 者稱之。
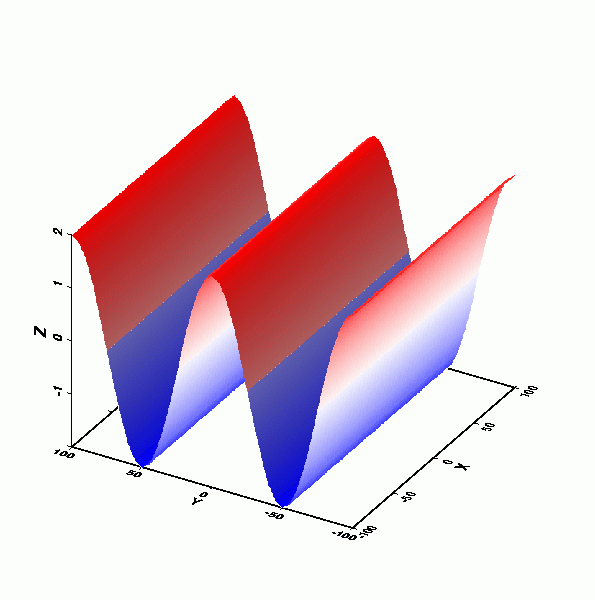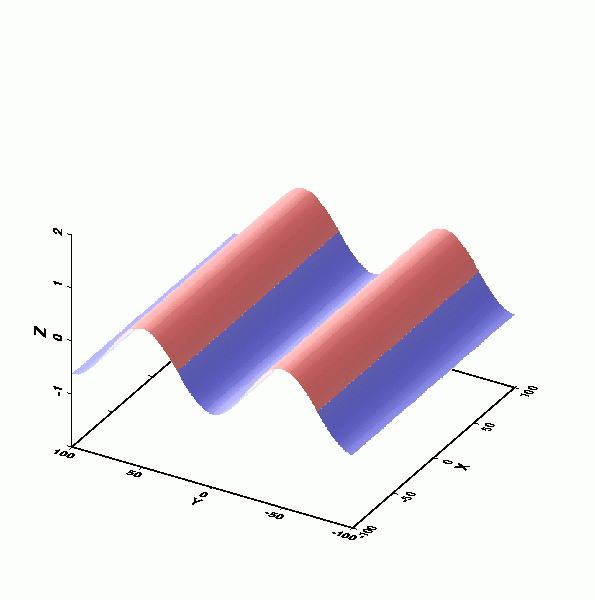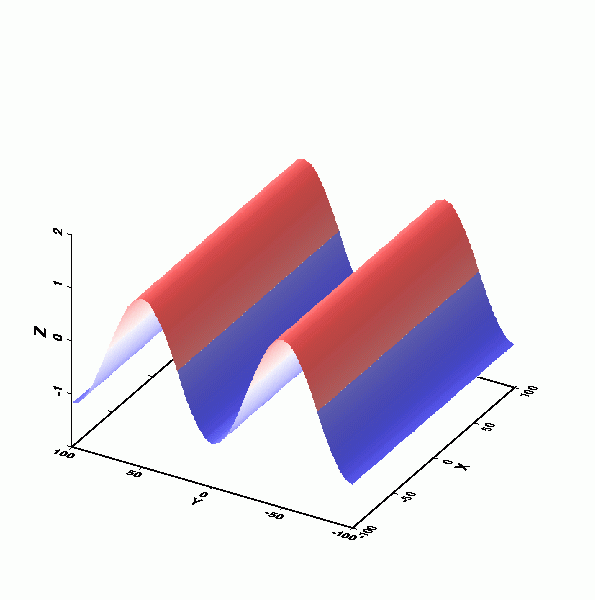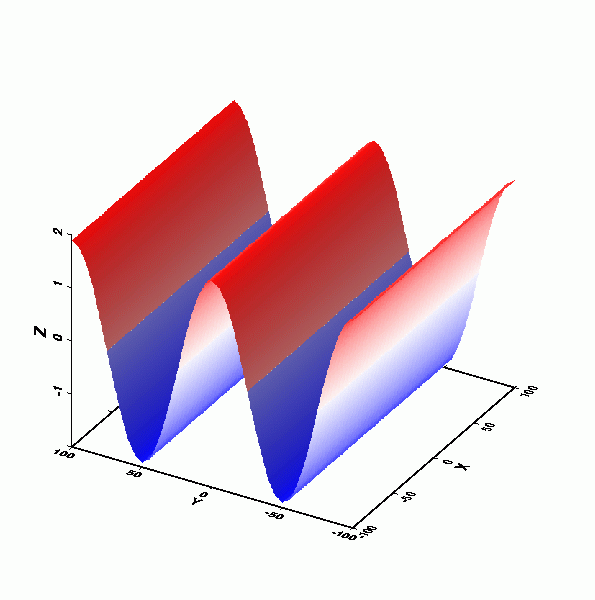

 水槽內的駐波:在一個週期內五個不同瞬間之水面振盪情形。
水槽內的駐波:在一個週期內五個不同瞬間之水面振盪情形。
摘自Thurman, H. V. (1993) "Essentials of Oceanography", 4th ed.。
中國古代的魚洗便是在盆中製造出駐波 (摘自 Youtube https://www.youtube.com/watch?v=13mBC-_7TRQ )
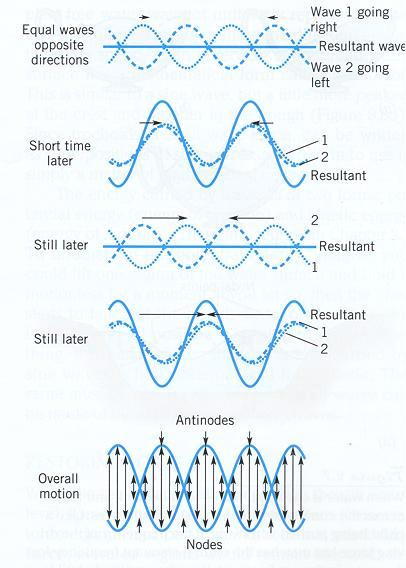
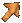 將兩組僅傳播方向相反的相同波列(一向左傳,另一則向右傳)相互疊加,如此
便產生了駐波。摘自Stowe, K. (1995) "Exploring Ocean Science", 2th ed.。
將兩組僅傳播方向相反的相同波列(一向左傳,另一則向右傳)相互疊加,如此
便產生了駐波。摘自Stowe, K. (1995) "Exploring Ocean Science", 2th ed.。
-
界面波(Interfacial wave):發生在二不同性質流體界面上的波動,例如空氣與水交界面上之水面波。
-
內波(Internal wave):當流體內部密度垂直分佈呈現層化構造時,流體內部也會出現波動。例如天空中常出現之帶狀透光高積雲或是卷積雲,便是高空氣團 流經下層另一種氣團時所產生的波動,有雲處為上升氣流,無雲處則為下沈氣 流。又如搭乘飛機時不免遭遇晴空亂流,飛機顛跛上下猶如船行波面,這些晴空亂流多是大氣中之內波。又如在海邊高處向海面眺望,常見海面水色相異處 呈帶狀分佈,或是海面漂浮物呈帶狀分佈,這些多表示水面下有較強之內波運動。(詳見本章第五節,內波)

 晴空常見之帶狀透光高積雲便是大氣中的內波。
晴空常見之帶狀透光高積雲便是大氣中的內波。
摘自Stowe, K. (1995) "Exploring Ocean Science", 2th ed.。

當輕(低鹽或是高溫)的海水漂浮在相對較重(高鹽或低溫)的海水之上時,海洋上層便呈現密度分層的情形,此時有利於發生內波。如上圖(b),船行這種水域,往往因為產生內波之尾跡而損失能量,致使船速變慢,早期由於不明瞭此現象因此造成船員恐慌,稱此為死水(Dead Water),Fridjof-Nansen在北極探測時便發現此現象(Nansen 1902),隨後Ekman(1906)以實驗証明和內波的關係。水下內波可以使近海面之水流形成帶狀的輻合或是輻散區,海面漂浮的物體便會在輻合區內排列成行(圖c)。 摘自Stowe, K. (1995) "Exploring Ocean Science", 2th ed.。
|
法國里昂ENS 物理實驗室(Physics Lab of ENS Lyon )仿Ekman內波實驗的影片 |
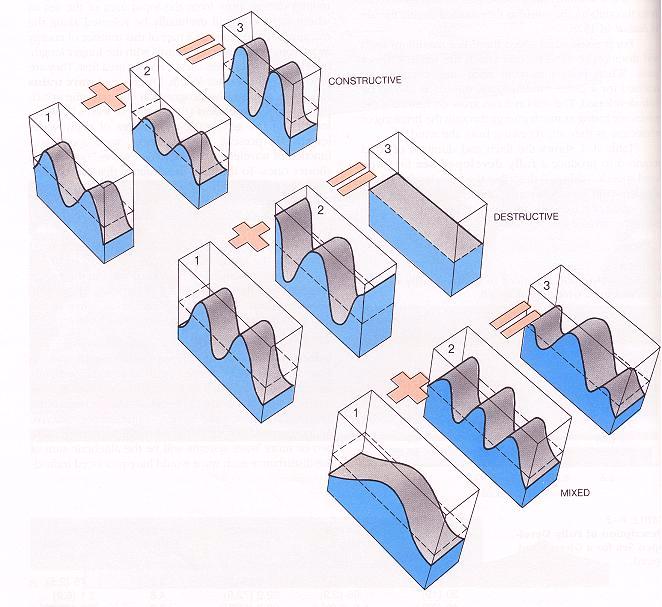
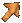 波浪疊加可以是建設性(上圖),破壞性(中圖)或是以上二者之混合型(下圖)。
摘自Thurman, H. V. (1993) "Essentials of Oceanography", 4th ed.。
波浪疊加可以是建設性(上圖),破壞性(中圖)或是以上二者之混合型(下圖)。
摘自Thurman, H. V. (1993) "Essentials of Oceanography", 4th ed.。
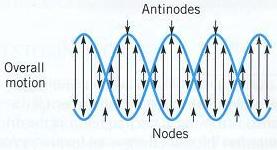 |
 駐波之奏點與節點。摘自Stowe, K. (1995) "Exploring Ocean Science", 2th ed.。 |
緣波(Edge waves): 波浪斜射邊界,入射波與反射波相疊加形成沿著平行於邊界方向傳的波形稱之為緣波。

 波浪斜射邊界,入射波與反射波的情形(左圖),以及入反射波疊加後形成
緣波的情形(右圖)。摘自Stowe, K. (1995) "Exploring Ocean Science", 2th ed.。
波浪斜射邊界,入射波與反射波的情形(左圖),以及入反射波疊加後形成
緣波的情形(右圖)。摘自Stowe, K. (1995) "Exploring Ocean Science", 2th ed.。
 |
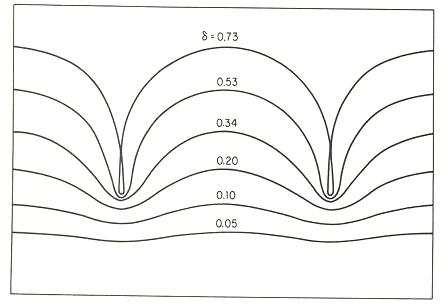 |
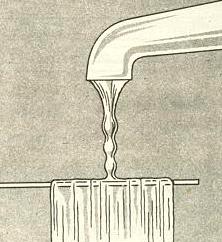
 如上左圖,在水龍頭下方放一片平板(或用手指頭亦可),可觀察到在水龍頭流出的水柱上會形成表面張力波的駐波。摘自Jearl Walker (1977) "The Flying Circus of
Physics", p93。上右圖則為在幾種不同尖銳度δ情況下(δ=0.73時,表面張力波發生「碎波」,此時水面波形相貼,在水下生成氣泡)根據有限振幅之表面張力波
(Crapper Wave)理論解所預測之波形。摘自Blair Kinsman (1984) "Wind Waves"。
如上左圖,在水龍頭下方放一片平板(或用手指頭亦可),可觀察到在水龍頭流出的水柱上會形成表面張力波的駐波。摘自Jearl Walker (1977) "The Flying Circus of
Physics", p93。上右圖則為在幾種不同尖銳度δ情況下(δ=0.73時,表面張力波發生「碎波」,此時水面波形相貼,在水下生成氣泡)根據有限振幅之表面張力波
(Crapper Wave)理論解所預測之波形。摘自Blair Kinsman (1984) "Wind Waves"。

 金龜子落在水面游泳時,或是水流經小樹枝,在其前方均會產生短波長的波痕,這些都是表面張力波。摘自Jearl Walker (1977) "The Flying Circus of
Physics", p87。
金龜子落在水面游泳時,或是水流經小樹枝,在其前方均會產生短波長的波痕,這些都是表面張力波。摘自Jearl Walker (1977) "The Flying Circus of
Physics", p87。
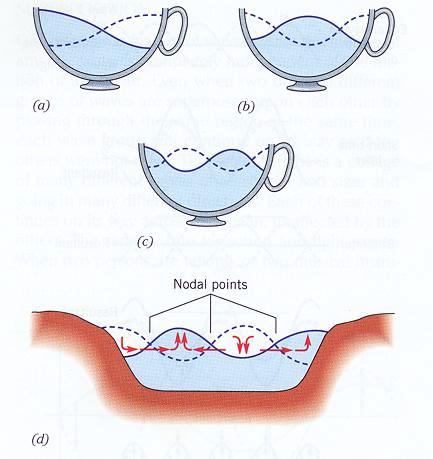
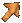 水面在茶杯裡振盪便是盪漾現象之一例(圖a至c)。圖d則為港池盪漾
現象之示意圖。摘自Stowe, K. (1995) "Exploring Ocean Science", 2th ed.。
水面在茶杯裡振盪便是盪漾現象之一例(圖a至c)。圖d則為港池盪漾
現象之示意圖。摘自Stowe, K. (1995) "Exploring Ocean Science", 2th ed.。

 |
 |