
本章教材始建於1998/9/17, revised: 2017/3/4
二、波浪運動
波速、色散現象:(對重力波而言)波長愈長波速(相速度)愈快,水深愈淺波速愈慢。 當水深大於一半波長時,稱為深水波(deep water waves),波速C = 1.25 √(L),式中C之單位為 m/sec,L則為公尺。當水深小於1/20波長時,稱為淺水波(shallow water waves),波速僅與水深有關, 其公式為C = 3.13 √(d),式中d為水深,單位為公尺。至於介於深水波與淺水波之間的則稱為中間水深波(intermediate water waves),波速
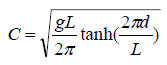 ,式中g為重力加速度。
,式中g為重力加速度。
 |
 |
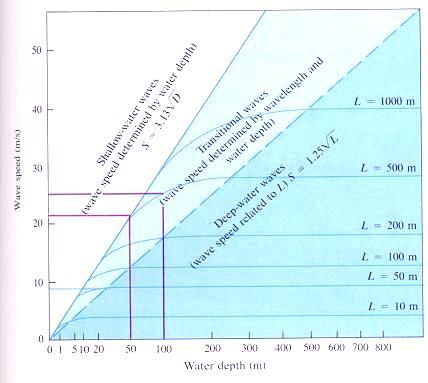
 水波(重力波)的相速度是波長以及水深的函數。
水波(重力波)的相速度是波長以及水深的函數。上 左圖摘自Thurman, H. V. (1993) "Essentials of Oceanography", 4th ed.。
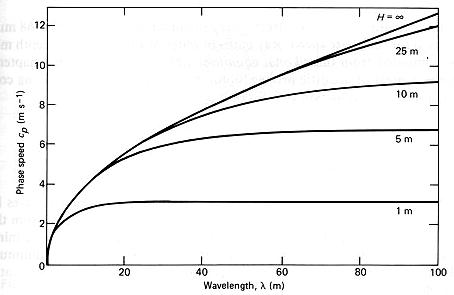
上 右圖則摘自Neumann, G. and Pierson, W.J., Jr. (1966) "Principles of Physical Oceanography"。
由於不同波長的波浪其傳播速度並不一樣,因此同一波源所產生之各種不同頻率(對應不同波長)波浪在向外傳播時會發生分離的現象,此即色散現象或稱離散現象(Dispersion,此名源自於光學,1666年牛頓發現太陽光經三稜鏡折射後可呈現彩色光,稱為光的色散現象,隨後水波亦沿用此名稱 )﹔例如颱風尚在遠海,但長湧已先至海濱﹔又如向水潭丟石產生圓形重力波,波群外緣為長波,內側的波波長則較短。波浪的頻率與波數間之函數關係式稱為離散關係(dispersion relation),各種不同的波(如表面張力波、重力波、彭卡瑞波、行星波等)均有各自不同的離散關係式。波浪學將波浪因頻率不同致相速度不同所造成的離散現象又稱為頻率離散(Frequency dispersion)。
 |
 |
 將小石子丟入水潭很快便產生了圓形重力波(左圖),過了一會兒圓形波向外擴展範圍更大,長波在外,短波在內(右圖)。因不同波長之水波波速不同,故波浪傳播過程中原始波列會發生按照波長大小前後散開排列的情形,
這就是波的色散現象(離散現象)。攝於臺大醉月湖。
將小石子丟入水潭很快便產生了圓形重力波(左圖),過了一會兒圓形波向外擴展範圍更大,長波在外,短波在內(右圖)。因不同波長之水波波速不同,故波浪傳播過程中原始波列會發生按照波長大小前後散開排列的情形,
這就是波的色散現象(離散現象)。攝於臺大醉月湖。
折射(Refraction)﹕同一頻率之波列傳播時,因波速快慢不一(受流或水深作用)導致波射線發生彎曲稱為折射。
(註:波射線 wave ray:向著波傳方向與波列相垂直之線稱之)
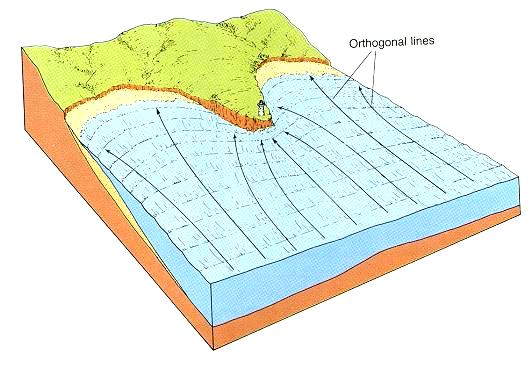
 波浪向岸傳播時,受水深不均勻影響發生折射現象之示意圖。
摘自Thurman, H. V. (1993) "Essentials of Oceanography", 4th ed.。
波浪向岸傳播時,受水深不均勻影響發生折射現象之示意圖。
摘自Thurman, H. V. (1993) "Essentials of Oceanography", 4th ed.。反射(Reflection)﹕波浪前進遭遇固體邊界時,為滿足水流只能平行於邊界面運動之限制,於是會產生向相反方向傳播的波浪,這就是反射現象。

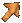 近岸水域入射波與反射波疊加形成的棋盤狀波形(86年6月攝自桃圓觀音海邊)。
近岸水域入射波與反射波疊加形成的棋盤狀波形(86年6月攝自桃圓觀音海邊)。繞射(Diffraction)﹕當波浪前進遭遇物體部份阻擋時,從物體側方通過之波浪亦會產生側向波傳至被物體遮蔽之水域,此即繞射現象,可用惠更斯原理(Huygens' principle)解釋。
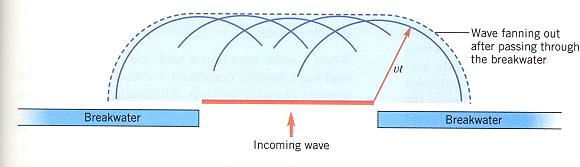
 惠更斯原理示意圖。摘自Stowe, K. (1995) "Exploring Ocean Science", 2th ed.。
惠更斯原理示意圖。摘自Stowe, K. (1995) "Exploring Ocean Science", 2th ed.。
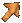 波浪繞射狀況。
摘自Stowe, K. (1995) "Exploring Ocean Science", 2th ed.。
波浪繞射狀況。
摘自Stowe, K. (1995) "Exploring Ocean Science", 2th ed.。
波浪繞射, 摘自Youtube Lesson 2 - Water Waves - Diffraction
水分子軌跡(Trajectory of particle)﹕深水波之水分子軌跡呈圓形,淺水波則為橢圓形。
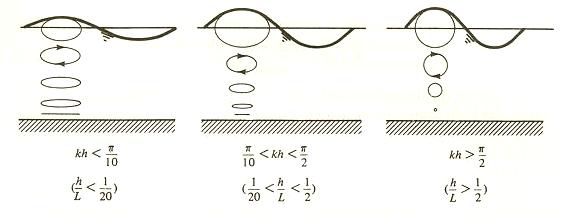
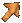 波浪作用下,水分子之運動軌跡,自左至右分別為淺水、中間水深以及深水情
況下之軌跡形狀,圖中之h為水深,k為波數,
k = 2π/L。摘自Dean R.G. and R. A. Dalrymple (1984) "Water Wave Mechanics for
Engineers and Scientists"。
波浪作用下,水分子之運動軌跡,自左至右分別為淺水、中間水深以及深水情
況下之軌跡形狀,圖中之h為水深,k為波數,
k = 2π/L。摘自Dean R.G. and R. A. Dalrymple (1984) "Water Wave Mechanics for
Engineers and Scientists"。
美國賓州州立大學Graduate Program in Acoustics網頁上有一幅很生動gif動畫(如下),舉例說明深水情況下,自由表面重力行進波(是將「自由、表面、重力、行進波」去除頓號後簡稱)由左向右傳,水面下水粒子運動情形,圖上橘色線則為水面以及水面下兩個水粒子之運動軌跡。(這個網頁上同時還有聲波、地震P波與S波等生動的動畫,很值得參閱)
摘自Acoustics and Vibration Animations (Daniel A. Russell, Graduate Program in Acoustics, The Pennsylvania State University)

波浪所造成之水分子運動狀態, 摘自Youtube Waves on the surface of water HD
波浪動量﹕在行進波的波峰與波谷之間區域,有時有水,有時則全為空氣。將此區域內水分子速度整體平均後可發現水分子整體是朝著波傳的方向流動(因此水波會在波傳方向上產生質量輸送),物理上「質量乘以速度」 即為動量,此平均動量稱為波浪動量(Wave momentum),波愈大則波浪動量亦愈 大,同時平均的流速也愈大。波浪動量對海岸動力學有很重要的意義,例如波傳至近岸淺灘發生碎波後,波高向岸一路衰減,因此波浪動量便會向岸遞減,同時質量輸送也向岸遞減,如此將造成平均水位向岸方向抬昇(稱為波致水位揚升,wave set-up),臺灣西南沿海在颱風季時常發生海水倒灌事件,除了漲潮與風揚作用可造成海水倒灌,波致水位揚升往往也是致災的另一項可能因素。
波群(Wave group)﹕波列通常成群向外傳播。最明顯的波群實例包括船波以及將石頭投入靜止水面後所形成的圓形波均是。每一波群內可能含括了很多個外觀波形,這一群波有時又統稱為一個波包(Wave packet),波包移動的速度即為群速度,也就是 波浪能量傳播的速度。
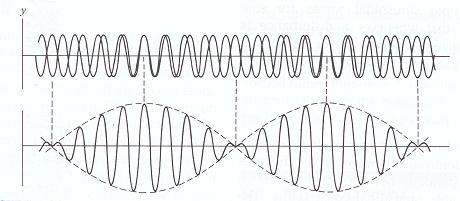
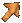 兩組波長稍微不同的波相疊加(上圖)以及疊加後形成波群的情形(下圖)。
摘自Keith Stowe (1987) "Essentials of Ocean Science",p91。
兩組波長稍微不同的波相疊加(上圖)以及疊加後形成波群的情形(下圖)。
摘自Keith Stowe (1987) "Essentials of Ocean Science",p91。
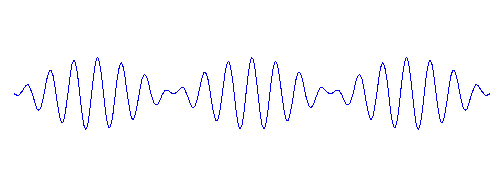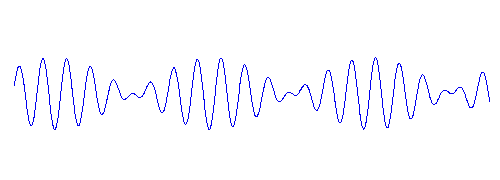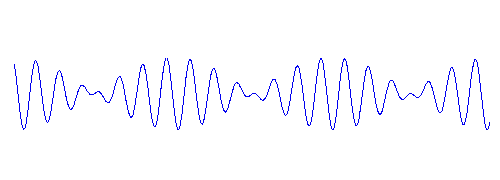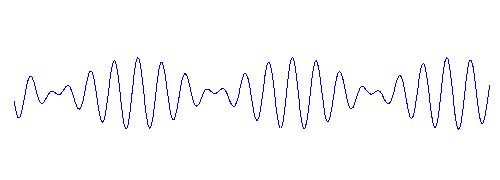
 模擬波包傳播的動畫(此例中波浪群速度為相速度的1/2。由外觀上看,因為個別波形跑得比波包要快,當個別波傳到波包前緣時似乎會消失不見,而在波包後緣則不斷會有新波生成,然後長大)。
模擬波包傳播的動畫(此例中波浪群速度為相速度的1/2。由外觀上看,因為個別波形跑得比波包要快,當個別波傳到波包前緣時似乎會消失不見,而在波包後緣則不斷會有新波生成,然後長大)。
波浪的群速度與外觀波形移動的速度(相速度)不一定會相等,二者相等者稱為非離散波(Non-dispersive waves),二者不相等者則為離散波(Dispersive waves)。水波為離散波,但水很淺時水波會近似於非離散波。深水重力波的群速只是相速的一半,所以隨著波包移動時會看到波包內的外觀波不斷由波包後方冒出來,然後向前移動,抵達波包前緣時又自行消失(如上圖)。 然而,深水表面張力波的群速卻大於相速,因此隨著波包移動時會看到個別波形會由波包前端生出,然後向後移,抵達波包後端時又自行消失。波浪預報估算大浪抵達的時間需根據群速度來計算。
都卜勒效應(Doppler effect):如果觀測者不動但波動所在之介質本身在平移流動,或是介質不動但觀測者相對在動,這時觀測者所觀察到波動之頻率便和二者皆不動時所觀察到者會不一樣,這就是都卜勒效應。課本中常以火車汽笛聲在駛近與駛離時音調變化為例來說明(如下即為一例)。
都卜勒效應,引自 Youtube Doppler Effect (car horn) VERY Noticeable!!
海洋上除了常有波浪外,海面下海水也會流動,因此海洋波浪所處之介質往往是在平移流動,是以我們不免要問:我們站在一個固定位置所觀察看到的波浪頻率(稱為外觀頻率或視頻率,apparent frequency,以n表示)和波浪真正具有的頻率(就是介質不平移流動情況下同樣波長之波所具有之頻率,稱為本質頻率,intrinsic frequency,以ω表示),二者間有何關係?如果以k表示波浪之波數(k=2π/L,L為波長),以Uk表示順著波形傳播方向上之海流流速分量(順波向為正,逆波向為負),那麼二者間之關係式為:
n = ω + kUk
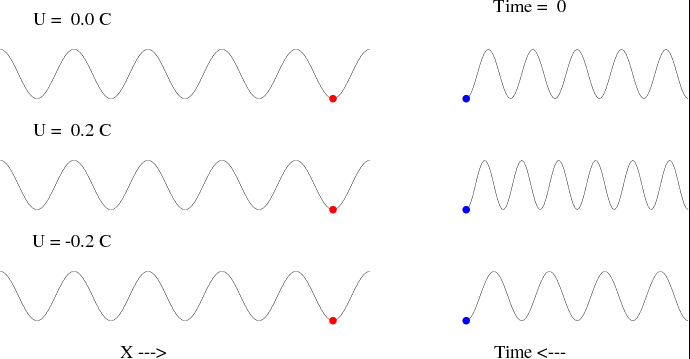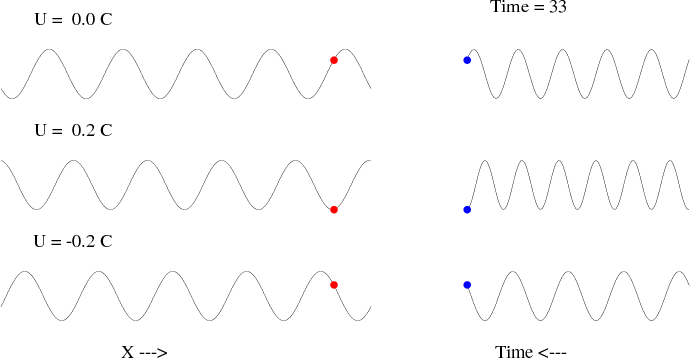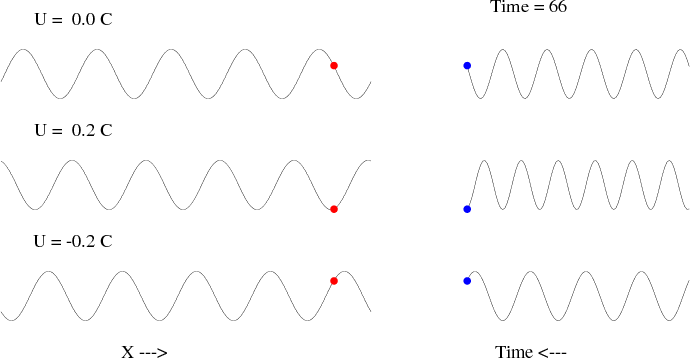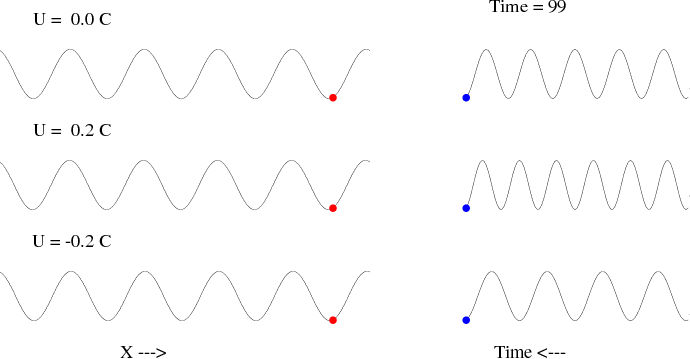
式中kUk這一項稱為都卜勒頻移(Doppler shift)。如上例,當汽車迎面馳來時,Uk為正,都卜勒頻移大於0,故觀測者所聽到的頻率(外觀頻率)便比汽車喇叭發出的頻率(本質頻率)為高;反之,當汽車馳離時,Uk為負,都卜勒頻移小於0,因此外觀頻率就變低了。同理我們也可以將此關係應用到在海上搭船的經驗上;如果你搭船出海過,一定會感受過頂浪航行時船比較顛簸,而順浪時則似乎風平浪靜;原因就出在頂浪航行時Uk為正(此時船是向著波而去,如果將船視為不動,便相當於是介質與波同向,均為朝向著船而來),外觀頻率變大;順浪航行時Uk為負,外觀頻率則變小;縱使顛簸的高程(波高)並沒改變,可是爬坡的時間(外觀頻率的倒數)卻大不相同,當然顛簸感(取決於加速度)就很不一樣了。下圖為展示水波都卜勒效應的動畫,圖左方有三組波長相同的行進波(相速度亦相同),最上者介質為靜止不動,居中者流向與波向相同,流速為水波相速度的20%,最下者則為流向與波向相反,流速亦為水波相速度的20%,紅點為在相同水平位置處所觀測到的波面;至於右側圖則為紅點所觀測到波面上下起伏之時間序列記錄,由此記錄可以一目瞭然看出不同情形下都卜勒頻移的差異。
非線性波(Nonlinear waves):
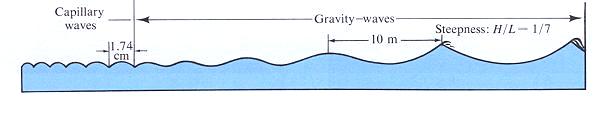
摘自Thurman, H. V. (1993) "Essentials of Oceanography", 4th ed.。
還記得本章一開始介紹表面張力波與重力波時用的這張圖(如上)嗎?在該圖圖例中說明:「當波長小於1.74cm時,表面張力效應較為重要,這種漣漪小波(表面張力波)具有圓形波峰以及V型波谷。當波長較長時,重力效應就變得比較重要,波浪能量比較小時波形和正弦曲線非常相近,可是當波浪能量不斷增加,重力波的波形也會漸漸改變,會變為波峰變尖而波谷則變平坦的形狀,當尖銳度達到1/7或以上時波形就無法支撐而會發生碎波。」不管是重力波的波峰變尖或是表面張力波波谷變尖都是因為波浪能量增大而水分子運動速度變快後所導致的效果,水分子運動速度變快暗示波浪場的非線性程度變大,而尖銳度正是顯示波浪場非線性程度的一項重要指標。
我們在前面所介紹水波的許多性質(例如疊加性、離散關係等等)主要都是針對線性波,也就是尖銳度近似於0的水波,這種波在波浪力學中被稱為小振幅波或微小振幅波,但是所謂的「微小振幅」並不是說「振幅微小」,而是指「波的振幅與其波長相比(就是尖銳度)十分微小」。當尖銳度夠大時水分子運動對自體本身所造成的平流效應(也就是非線性作用)便會變得比較顯著,這種影響在深水重力波領域會造成水波的波峰變尖而波谷則變平坦(如上圖,之所以會呈現這種倒餘擺線-trochoid型態的波形,就是因為波浪作用下水分子運動軌跡為圓形所對應的,對此有興趣者可參閱餘擺線波trochoidal wave)。波浪力學將深水、尖銳度變大後以攝動法(perturbation method)求出的自由表面有限振幅重力波(free surface finite-amplitude gravity waves)理論解稱為Stokes波,該波便具有尖峰緩谷的波形,同時其相速度大小除與波長(或週期)有關外,亦與尖銳度的平方呈正比關係;換言之,對同樣波長的水波,振幅大者其相速亦較快,這種因振幅不等而造成的離散作用在波浪學中被稱為振幅離散(Amplitude dispersion);與前述之頻率離散是由完全不同的物理效應所造成的。
水波由深水傳入淺水海域(所謂深水、淺水是由水深 d 與波長 L之比值來判斷,d/L > 0.5為深水,d/L < 0.05則為淺水),水深逐漸變淺,當d/L < 0.5時水深對水波的影響-稱為淺化效應(shoaling effect),便會逐漸顯現出來,水波在淺化過程中頻率並不會改變,但相速度以及波長均會減小,因此波能密度(每單位面積海面之波浪總能量,見第四節)便會增大,是以波高也就變大(由於水波群速度在由深水至淺水階段的初期反會加速,因此波高反會先行減小,最多可減小10%,而後便隨水變淺而遞增),而波的尖銳度當然也同步放大(非線性度加大),波形便不斷陡化;另外當水很淺時,水波非線性效應強烈,波面上每一點之波形移動速度會與該點至海底距離之平方根成正比,如此一來波峰(移動最快)便會逐漸追上前方的波谷(移動最慢)而形成近似水牆的形狀,強烈者波峰甚或會越過波谷而形成崩捲型態,促發碎波(見第三節);碎波後水波能量大量消散。
在坡度十分平緩的淺水海域中,受到非線性作用影響的水波其波形理應不斷陡化,如果促成陡化的效應作用不是很強烈,那麼就仍有可能可以藉助頻率離散作用將這部份效應散播出去而使波形保持穩定不變,如此便允許自然界出現一種很特別的波動-孤立波(Solitary wave)。
孤立波(Solitary wave): 孤立波是一個其波形只有一個波峰而其波長則為無限長的非線性波動,如以孤立波的群速跟著孤立波同步移動則可見其波形與波高均不會隨時間而改變。
孤立波最早是由180多年前蘇格蘭造船工程師John Scott Russell發現的。Russell因工作關係常需觀察駁船運作狀況,1834年8月某日他在蘇格蘭愛丁堡附近尤寧運河(The Union Canal)觀看由馬拉縴行進的駁船,發現當駁船突然停止時,船頭前方水面出現了一道高約1-1.5英呎的平滑隆起,寬度約30英呎,這道水面隆起出現後會繼續向前移動,Russell好奇便騎著馬跟著平滑的隆起水面前進,發現水面隆起形狀以及移動速度幾乎不變,移動速度約每小時8-9英哩,他跟著這道水面隆起走了1-2英哩,直到運河一處彎曲段水面隆起消失不見才中止。Russell認知到這個現象在科學上有重要性,隨後便在自家院中建水槽投入研究,1844年將研究成果撰寫論文發表,Russell稱此種波為「平移波」(Wave of Translation),現今則稱為孤立波。
 |
|
簡言之,孤立波是非線性作用下波長為無限長的一種水波,這種型式的波動可用在許多種物理學次領域中,由於孤立波又具有和粒子類似的特性所以往往又稱為孤子波(soliton)。下圖以動畫顯示二孤立波相對交會之互撞過程,結果是各走各的,不發生作用。
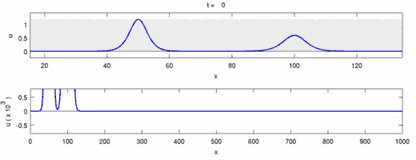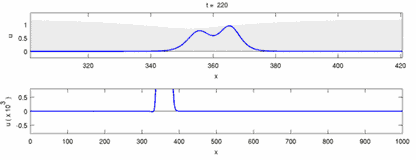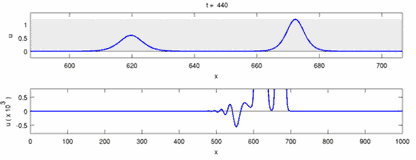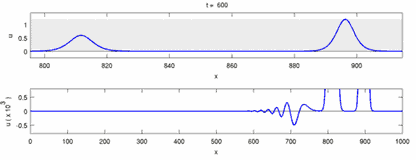 |
|
我國有名的錢塘涌潮(tidal bore)就是一種孤立水波,當涌潮傳入錢塘江河口時原先單一波峰的潮波還會裂解成為波列(由許多波組成),波列中的眾波會由大而小按照振幅與波長的大小順序排列(因為大的波跑得快,小的波跑得慢造成的),而每一個波的波形都和孤立波近似,此種波列也統稱為孤子波(solitons)。 孤子波型態的內波則稱為孤子內波(Internal soliton)。
 |
(Photo from Nature v. 376, 3 Aug 1995, pg 373) |
 |
 |
 |
 |
| 自然界的孤立波-錢塘江河口孤子波型態的涌潮 |
(摘錄自中視大陸尋奇--錢塘觀潮) |

(引自https://kknews.cc/culture/kyjogp.html)
唐 孟浩然 「與顏錢塘登樟亭望潮作」
百里聞雷震,鳴弦暫輟彈。
府中連騎出,江上待潮觀。
照日秋雲迥,浮天渤澥寬。
驚濤來似雪,一坐凜生寒。
 -
- |
 |

 今日蘇格蘭愛丁堡附近尤寧運河(The Union Canal)仍有由馬拉縴行進的觀光遊船。摘自
今日蘇格蘭愛丁堡附近尤寧運河(The Union Canal)仍有由馬拉縴行進的觀光遊船。摘自