三、密度、σt與比容

海水密度(ρ)是海水鹽度(S)、溫度(T)以及壓力(P)的函數(這個函數式稱為狀態方程式，equation of state)。 密度會隨鹽度增加、溫度減少以及壓力增加而增加，反之則減少， 即$\rho \propto S, T^{-1}, P$。當我們得到海水之溫、鹽及壓力等數值後，便可根據海水的狀態方程式計算出海水的密度。在cgs單位下，海水的密度數值大小多為1.0xxxx... (g/cm3,純水密度近似為1，表面海水之最大值約為1.028)，為了便於書寫以及節省數字空間計， 百年前海洋學猶在萌生期時即採用σ符號來代替ρ，即σstp = (ρstp-1) x 1000，式中 ρstp稱為現場密度，表示在現場之S,T,P 情況下之密度，這種習慣用法延用至今。同法，以 σ0表示在海面(一大氣壓下)，0°C情況下之海水密度。而σt 則為在一大氣壓條件下以現場之S,T所得出之密度，是以σt 又稱為條件密度，這是物理海洋學表示海水密度經常使用的單位(其因次為kg/m3)，σt= (ρst0/ρm - 1) x 1000，式中ρst0亦可寫成ρ(S,T,0)，為以現場鹽度與現場溫度代入海水的狀態方程式，但壓力則定為一大氣壓，如此算出之海水密度稱之；此外，在上式中 ρm= 999.975 kg/m3，為純水之最大密度。在不很深(即深度在1000公尺以內)的情況下，海水之條件密度與位密度(σθ，Potential density)二者數值甚為相近，因此也可直接用前者作為估算海水穩定度(以及浮力頻率，參閱第七章-第五節內波)之根據；但如需要精確的數值，則需使用位密度來計算。位密度之計算得經兩道手續，首先計算出位溫(Potential temperature，θ )，然後將θ、現場鹽度以及參考壓力等數值再代入海水的狀態方程式即可算出位密度，有關計算方法可參閱Gill (1982)。

為便於讀者應用，玆摘錄海水之狀態方程式如下(Gill 1982)﹕
首先計算純水之密度，即鹽度S = 0 (單位 psu)時之密度，計算方程式為
 ρw=999.842594 + 6.793952×10-2T - 9.095290×10-3T2 - 1.001685×10-4T3 - 1.120083×10-6T4 + 6.536332×10-9T5，
式中T表示溫度(單位$^\circ C$)。其次則為ρ(S,T,0)之方程式(壓力P = 0, 單位為bar)，
 ρ(S,T,0) = ρw +S (0.824493 - 4.0899×10-3T + 7.6438×10-5T2 - 8.2467×10-7T3 + 5.3875×10-9T4) + S3/2 (-5.72466×10-3 + 1.0227×10-4T- 1.6546×10-6T2) + 4.831410-4S2

最後得出壓力為P bar時之密度ρstp為 ρ(S,T,P) = ρ(S,T,0)/(1-P/K(S,T,P))，
式中之K(S,T,P)又要經三道手續計算﹕
Kw = 19652.21 + 148.4206T - 2.327105T2 + 1.360477×10-2T3 - 5.155288×10-5T4
其次則為
 K(S,T,0) = Kw +S (54.6746 - 0.603459T + 1.09987×10-2T2 - 6.1670×10-5T3) + S3/2(7.944×10-2 + 1.6483×10-2T - 5.3009×10-4T2)
最後得出
K(S,T,P) = K(S,T,0) + P(3.239908 + 1.43713×10-3T + 1.16092×10-4T2 - 5.77905×10-7T3) + PS(2.2838×10-3 - 1.0981×10-5T - 1.6078×10-6T2) + 1.91075×10-4PS3/2 + P2(8.50935×10-5 - 6.12293×10-6T + 5.2787×10-8T2) +P2S(-9.9348×10-7 + 2.0816×10-8T + 9.1697×10-10T2)。

如此求出之密度其單位為kg/m3，另外還有三個數值可用作檢驗上述公式是否正確之參考依據，即 ρ(0,5,0) = 999.96675，ρ(35,5,0) = 1027.67547以及 ρ(35,25,1000) = 1062.53817。 根據以上這些公式便可由CTD實測之壓力、溫度及鹽度等資料算出海水密度；至於位溫之計算公式則見Gill(1982, p602)。

純水在4°C時密度最大，S = 24.7 ‰ 時最大密度則發生在-1.332°C (冰點亦在此)。在上層海洋中，海水密度隨溫度、鹽度與壓力變化「大致上」有如下之關係﹕即，溫度每減少5°C時σ密度會增加1，而鹽度每增加1 0/00 時σ密度亦會增加1，但深度(壓力)則為 每增加200公尺(約20個大氣壓)時σ密度才會增加1。

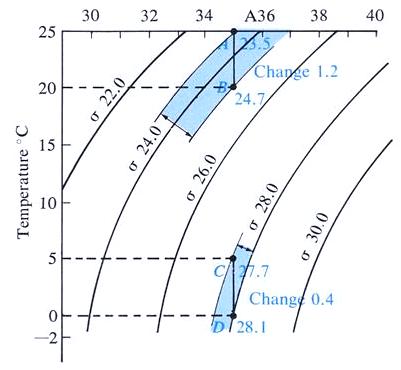
T-S圖是觀察海水密度與溫、鹽值
之間關係最方便的工具。左圖橫軸
為鹽度，單位為psu，暖海水降溫
5度密度增加1.2，但冷海水降溫5度
密度只增加了0.4，顯示密度與溫度
之關係並非簡單的線性比例。摘自
Thurman, H. V. (1993) "Essentials of
Oceanography", 4th ed.。

此外，物理海洋學上往往要用到 $\frac{1}{\rho}$，因此又定義了 $\alpha = \frac{1}{\rho}$，稱為比容(Specific volume)，其意義為單位質量海水所具有之體積，而σt 也是常出現的物理量。


1998/ 8/6 (minor revision: 2017 3/7)