本章教材始建於1998/9/17, revised: 2017/3/4
四、風浪
摘自Yih C.-S. (1980) "Stratified Flows"，Academic Press。
五代南唐 馮延己(903-960)
謁金門·風乍起
風乍起，吹皺一池春水。閑引鴛鴦香徑裡，手挼紅杏蕊。 鬥鴨闌幹獨倚，碧玉搔頭斜墜。終日望君君不至，舉頭聞鵲喜
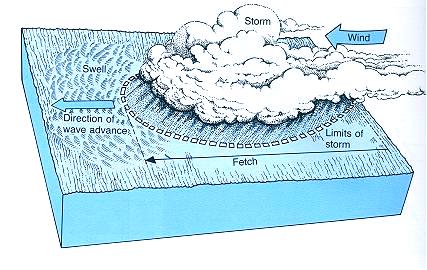
南唐馮延己「謁金門·風乍起」有詞云﹕「風乍起，吹皺一池春水」。可見古人早知風與浪具有密切的因果關係，但風浪生成、發展、衰減的完整理論迄今猶未發展到非常完善的境界。風浪成長係受風速、風域(Fetch，指順風方向吹風區域之長度距離 )以及吹風延時(Duration，指風持續吹襲的時間長度 )等三項主要的外在因子(External parameters)所控制，在其發展過程中又受不同頻率波浪間會發生能量交換作用(稱為非線性交互作用，會使波浪場能量轉移給低頻成份波)之影響，是以波浪場由風場不斷獲得的能量就逐漸往波浪能譜中低頻率波段移動、累積，因此波高漸漸增大而外觀波長也漸漸增長。
 |
|
 |
|
風浪預報法則﹕蒲福風級表、SMB波浪預報圖表、波浪模式
通常風浪之浪高、波長(或是週期)與風速、風域以及吹風延時等三因素大小呈正比，海面上風浪與風由於具有相期相伴的關係， 故一般均將二者綜合稱為海況，並沿用1805年由愛爾蘭裔的英國皇家海軍軍官蒲福(後來晉升為海軍少將，Rear Admiral Sir Francis Beaufort)所設計之蒲福風級表(如下表)來描述海況大小(蒲福風級表在1838年採用時僅有十二級，目前已延伸至十七級)。
摘自中央氣象局
https://www.cwa.gov.tw/V8/C/K/Encyclopedia/nous/overview_list.html#overview-09
以下為蒲福風級表0至12級所對應之海面實景照片(引自於National Weather Service, Observing Handbook No. 1, Marine Surface Weather Observations 電子書)，海上作業可參考比對：
蒲福風級 0級： 無風Calm，10m高風速 < 0.3m/s， 海面如鏡。
蒲福風級 1級：
軟風Light air，10m高風速 0.3-1.5 m/s，海面有鱗狀波紋，波峰無泡沫。
蒲福風級 2級：
輕風Light breeze，10m高風速 1.6-3.3 m/s，微波明顯，波峰光滑未破裂。
蒲福風級 3級：
微風Gentle breeze，10m高風速 3.4-5.4 m/s，小波，波峰開始破裂，泡沫如珠，波峰偶泛白沫。
蒲福風級 4級：
和風Moderate breeze，10m高風速 5.5-7.9 m/s，小波漸高，波峰白沫漸多。
蒲福風級 5級：
清風Fresh breeze，10m高風速 8.0-10.7 m/s， 中浪漸高，波峰泛白沫，偶起浪花。
蒲福風級 6級：
強風Strong breeze，10m高風速 10.8-13.8 m/s，大浪形成，白沫範圍增大，漸起浪花。
蒲福風級 7級：
疾風Near gale，10m高風速 13.9-17.1 m/s，海面湧突，浪花白沫沿風成條吹起。
蒲福風級 8級：大風Gale，10m高風速 17.2-20.7 m/s，巨浪漸升，波峰破裂，浪花明顯成條沿風吹起。
蒲福風級 9級：
烈風Strong gale，10m高風速 20.8-24.4 m/s，猛浪驚濤，海面漸呈汹湧，浪花白沫增濃，減低能見度。
蒲福風級10級：
暴風Storm，10m高風速 24.5-28.4 m/s，猛浪翻騰波峰高聳，浪花白沫堆集，海面一片白浪，能見度減低。
蒲福風級11級：
狂風Violent storm，10m高風速 28.5-32.6 m/s，狂濤高可掩蔽中小海輪，海面全為白浪掩蓋，能見度大減。
蒲福風級12級：
颶風Hurricane，10m高風速 > 32.7 m/s，空中充滿浪花白沫，能見度惡劣。
以上12幅圖均引自：National Weather Service, Observing Handbook
No. 1, Marine Surface Weather Observations,
US National Weather Service。
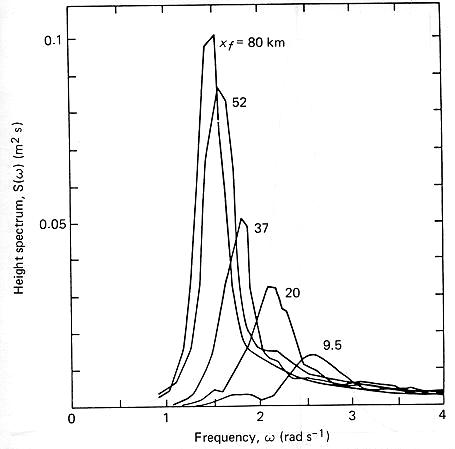
蒲福風級表可以看成是一種簡化的、經驗式的波浪預估法則。在開闊幾乎不受限的大洋海域，若風域大、吹風延時夠長，那麼由蒲福風級表根據風速大小來推估浪高往往也能得到不錯的粗略結果。然而如果為了特定目的想要得到較精準的波場參數數值(例如波高、週期等)，特別是在風域受限或是吹風延時變動的情形下，那麼蒲福風級表就力有未逮了。二次大戰期間，盟軍為了在北非以及歐洲登陸作戰所需，在美國加州由Sverdrup與Munk等帶領研究人員發展波浪預報方法，他們了解到實際海面的波形紛紜多變(如下圖)，必需藉由統計方法來處理，因此建立了以統計代表波的方式描述波浪場的方法，然後將外海與實驗水槽中量測到的統計波高數值與風速、風域以及吹風延時等外在參數相聯結，建立了代表波波高、週期與風速、風域和吹風延時間的經驗公式 ，並以此作為風浪預報之根據。
強風吹掠下海面波浪狀況
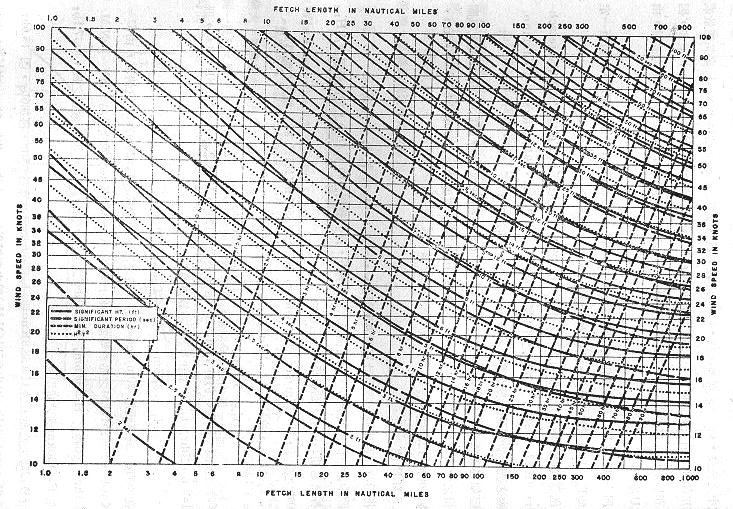
二次大戰戰後，Sverdrup與Munk 在1947年將戰時所發展的波浪預報公式發表，1952年 Bretschneider (抗戰時期Bretschneider曾在我國大陸戰區服役，任職美軍氣象官) 將Sverdrup與Munk 的公式再予完善並製成圖表(如下圖)，後來這一套波浪推算的作法就稱為SMB法。對SMB法有興趣者可參閱：REVISIONS IN WAVE FORECASTING (Bretschneider L. , 1957), On the prediction of wave parameters using simplified methods , (有step by step 說明如何使用Bretschneider nomogram)等。
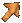
以代表波參數方式來描繪波浪場還是過於粗糙，並不符波浪研究以及造船與海洋工程方面的需求，是以統計波浪學乃因應而生。早在上世紀50年代初，海洋學界一些前輩學者們(例如W.J. Pierson)便認知到對於探討真實世界紛紜混亂的海洋波浪場，傳統決定論的(deterministic)推衍方法近乎已無能為力，必需藉助統計方法；他們提出了四項重要的觀點，分別是：(1)處理紛紜的海面波浪必需使用特別的統計方法，如隨機過程(stochastic process)方法；(2)波浪本身是流體的一種運動現象，因此統計結果也需遵循流體力學基本方程式的規範；(3)波浪能譜是一種可以描繪紛紜海面波浪場的有力工具；以及(4)使用多變量機率函數(multivariate probability function)描述紛紜海面波浪之時-空構造時，如果波浪場之統計是處於平穩狀態(stationary)下，那麼這些機率函數將與時、空之絕對座標無關，僅與不同時、空點座標之相對距離有關(參見Kinsman, B., 1965, Wind Waves: Their Generation and Propagation on the Ocean Surface; Dover Earth Science, Paperback – June 19, 2012)。前輩學者們引用統計學觀念所提出的這些洞見奠定了近代統計波浪學研究發展的基礎。
統計波浪學是將紛紜海面看成為由無限多組不同頻率(對應之波數由波浪離散關係決定)、不同傳播方向(決定波數向量的方向)的成份波所疊加組合而成，這些成份波的初始相位假設是在0與360度之間均勻分布的隨機變數(random variable)，而各成份波之振幅平方除以頻寬(此商值稱為能譜密度-spectral density)後按頻率排列即為波浪能譜(也有的模型是將成份波的初始相位與振幅相結合，共同組成為隨機變數)；對時-空中任意一個固定點而言，由這種波浪模型所組出的水位結果將不再是一個固定數值(因為成份波的初始相位是隨機變數)，而會是一個分布在正負無限大之間、具有無限多種可能性的數值，我們並無法確知這個數值應當是多少，但可以統計它的機率分布狀況，而後者則與波浪能譜有關；藉由這樣的模型我們才能更合理地將理論與真實的紛紜海面狀態相聯結。在說明現代波浪預報系統使用的方法前，我們需要先介紹一下波能密度以及另一個很特別、也不易體會、有點抽象的物理量--波作用量(Wave action)。
波能密度(Wave energy density)：我們在述及波浪狀況時有時會說到「波能」一詞，其實這只是對全稱「波能密度」的簡稱。波能密度是指在單位面積海面上之水波位能與海面-海底間整個水柱內波致運動動能的總和，因此波能密度的因次(量綱)是「能量/面積」，所以稱為「能量的密度」--波能密度。
波作用量(Wave action)：在古典力學中，作用量 = (動能-位能)x時間 (指系統作用的時間)，參閱「林琦焜 最小作用量原理 數學傳播35卷1期, pp. 15-28 」。如波能密度為E，水波的本質頻率(Intrinsic frequency, 也就是無水流時波的頻率)ω，則水波的波作用量密度(A)定義為：A = E/ω，其因次為「能量x時間/面積」。這個物理量最早是1962年由Sturrock P.A. 所提出，隨後1968年 Bretherton 與 Garrett 証明在無摩擦、水深不均勻且有水流的狀況下，小振幅水波的波作用量密度是一個具有保守性的物理量(如下式)，
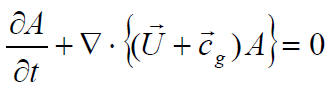
上式中，
與
分別為介質的流速以及水波之群速度
(參見Wave
action: continuum mechanics)。然而，我們還可以從另外的角度來看波作用量；1959年Starr (Starr, V.P.
1959, Hydrodynamical analogy to E = mc2 . Tellus, 11,
135-138.)導出小振幅水波具有E = MC的關係，式中M為水波的波動量密度，C為波(在沒有水流情形下)的相速度，由於C=ω/k，因此可得出
A = E/ω
= M/k；因為k=2π/L，所以可知波作用量相當於一個完整波長內的波動量之總和。換言之，當水波波列在不均勻的介質(例如水流與底深分布均為不均勻)中傳播時，雖然波長在空間中會發生變化，但每一個波形涵蓋範圍下所具有的波動量總量卻維持不變，從這個角度可以比較容易體會波作用量密度守恆的意義。
波浪預報方程式：現代波浪預報主要是根據波作用收支方程式(如下式)或波能收支方程式(下式亦可轉化成波能方程式)來建立數值模式，然後代入現報以及預報的風場變化來推估波浪的傳播、生長與衰退的過程，以進行波浪預報。
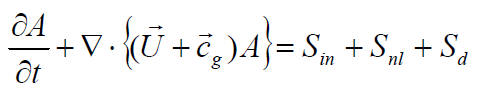
上式等號右側三項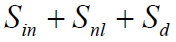
稱為源函數(source
function)，其中第一項為風驅效應(包括線性成長項、指數成長項，二者均和風浪生成的物理機制有關)；第二項為各成份波之間的非線性交互作用，其效用是會使波能在不同頻帶間轉移；而第三項則為消散作用項，包括有碎波效應、亂流混合以及底部摩擦等作用。通常將SMB法之類簡化的、完全不考慮波與波非線性交互作用的預報模式稱為第一代波浪模式，而採用波作用(或波能)收支方程式建立的波浪預報系統則稱第二代(非線性交互作用項是以參數化之簡化方式估算)或是第三代波浪模式(以完整的方式處理非線性交互作用項)。此外式中
A = A(ω,θ；x,y,t)，係將A拆解為由許多不同頻率(ω)、不同傳播方向(θ)的成份波組合而成，成份波數量越多預報能譜的頻率解析度就越高，加以空間步長也越小越好，而時間步長也得因應變小，因此電腦記憶體就要很大，而計算速度也要很快才行。廣用的第三代模式包括有
WAM, SWAN, WAVEWATCH III等。中央氣象局海象測報中心波浪預報使用的也是第三代模式，下圖即為其每日輸出成品一例。
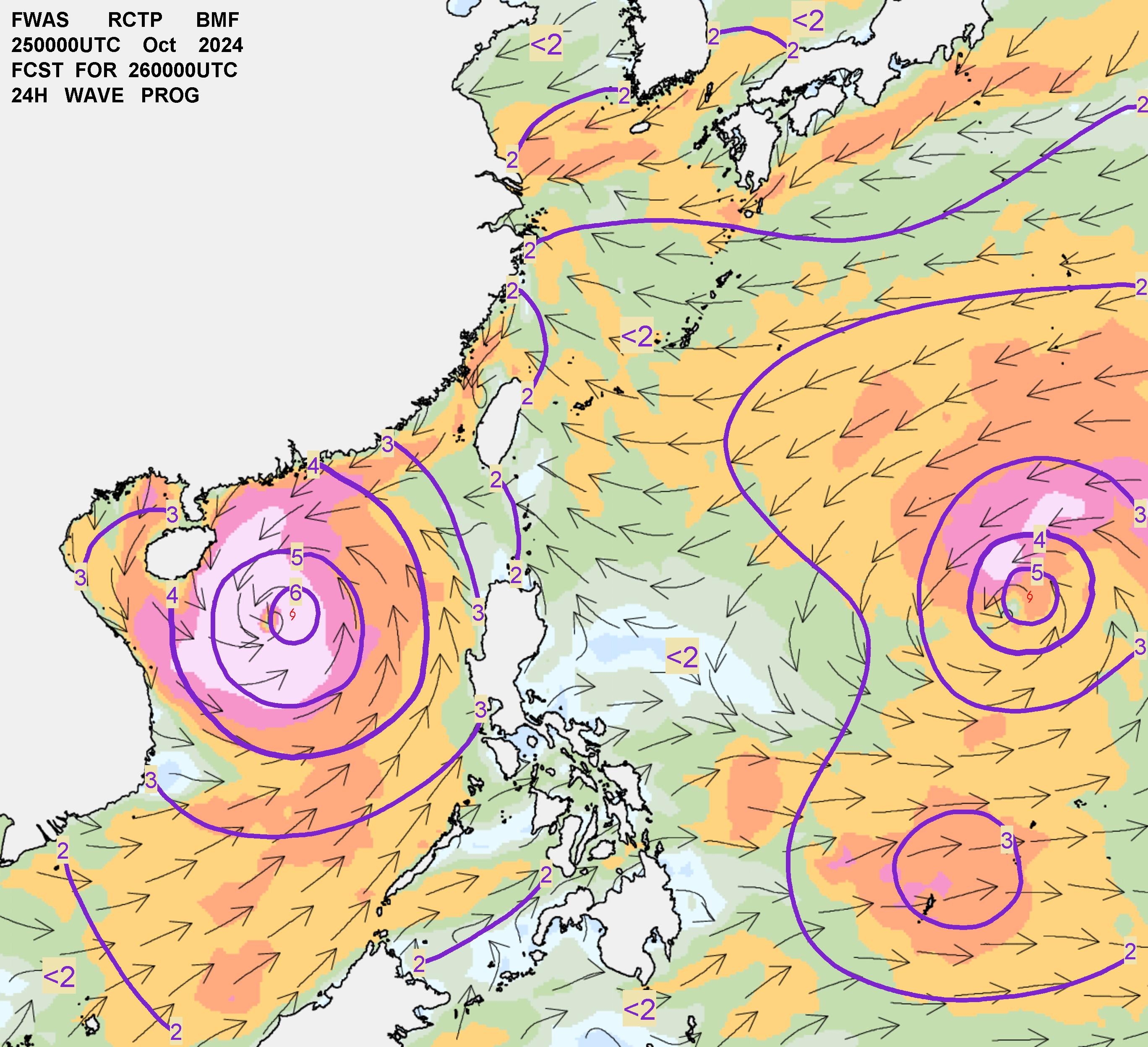
最大波有可能到達上述波高的兩倍，使用此圖需加以注意。 (摘自中央氣象署)
 |
 |